Note: This is less of a blog post and more of a running commentary on a project I have conceived. I have a long way to go on it but I hope you enjoy the journey.
I’ve been thinking about computers I have seen at places like The National Museum of Computing in the UK or the Computer Museum of America here in Metro-Atlanta. One of the things that has always challenged me is how to benchmark computers against each other. For instance, we know the Cray 1A at the CMoA had 160 Megaflops of computing power, while a Raspberry Pi 4 has 13,500 Megaflops of computing power according to the University of Maine. What can you do with a megaflop of power however? How does that translate in the real world.
I’m considering a calculation matrix that would use one of two metrics. For older computers, how many places of Pi can they calculate in X amount of time. Say 100 seconds? For newer computers, how long does it take for the machine to calculate Pi to 16 Million places. Here are my early examples:
Pi to 10,000 Places on Raspberry Pi
| Computer | Processor | RAM | Elapsed Time | How Calculated |
| Raspberry Pi Model 3 | ARM Something | Something | 6 Min 34 Sec 394 Seconds | BC #1 (Raspbian) |
| Raspberry Pi Model 3 | ARM Something | Something | 2 Min 15 Sec 135 Seconds | BC #2 (Raspbian) |
| Raspberry Pi Model 3 | ARM Something | 0 Min 0.1 Sec | Pi command |
Pi to 16,000,000 Places
| Computer | Processor | RAM | Pi to 16M Places Time | How Calculated |
| Lenovo Yoga 920 | Intel Core i7-8550U CPU @ 1.8 GHz | 16 GB | 9 Min 55 Sec 595 Seconds | SuperPi for Windows Version 1.1 |
| Lenovo Yoga 920 | Intel Core i7-8550U CPU @ 1.8 GHz | 16 GB | 0 Min 23 Sec | Pi command |
| N4BFR Vision Desktop | Intel Core i7-12700K CPU @ 3.6 GHz | 32 GB | 3 Min 15 Sec 195 Seconds | SuperPi for Windows Version 1.1 |
| Raspberry Pi Model 3B+ | ARM 7 Rev 4 (V71) | 1 GB | 6 Min 03 Sec 363 Seconds | Pi command |
Tools I am considering to use will be an issue because I want consistent performance across operating systems. Efficiency will be an issue because I will want something that computes at roughly the same speed for windows as for Unix.
- SuperPi for Windows 1.1 was the first I came across and it seemed to be pretty straightforward that would run on many versions of Windows I came across.
- Moving on to a calculator I could use in Unix, I found this John Cook Consulting Website that had a couple of calculations using the BC program. I found the results inconsistent on the Lenovo Yoga 920
BC Calculation 1: time bc -l <<< "scale=10000;4*a(1)" BC Calculation 2: time bc -l <<< "scale=10000;16*a(1/5) - 4*a(1/239)"
I then found the Pi command on pi that might be more consistent with what I need.
$ time pi 10000Pi Calculations on Lenovo Yoga 920
Windows time is reported by SuperPi. BC time is “Real” time reported by process.
| Pi Calculated to X Places. X= | Windows Time | BC ` | BC 2 | Pi Command |
| 10K (Pi Compairison) | 1 Min 45 Sec | 0 Min 32 Sec 0 Min 35 Sec | 0.09 Sec | |
| 20 K | 3 Min 22 Sec | 0. | ||
| 50K | Incomplete after 15 minutes | |||
| 128K | 0 Min 01 Sec | Incomplete after 60 Minutes | ||
| 512K | 0 Min 08 Sec | |||
| 1 M | 0 Min 16 Sec | |||
| 8 M | 3 Min 05 Sec | |||
| 16 M | 9 Min 55 Sec | 0 Min 23 Sec |
So using BC as a method of calculating does not seem to scale.
Coming back to this a few days later, I may have a partial solution. This will limit the use of this on older machines, but should be fairly consistent with newer ones. I plan to do the calculation with a script in Python 3. This should allow for roughly similar performance on the same machine to make results more comperable.
Python3 Downloads: https://www.python.org/downloads/release/python-3105/
Python3 methods for calculating Pi: https://www.geeksforgeeks.org/calculate-pi-with-python/
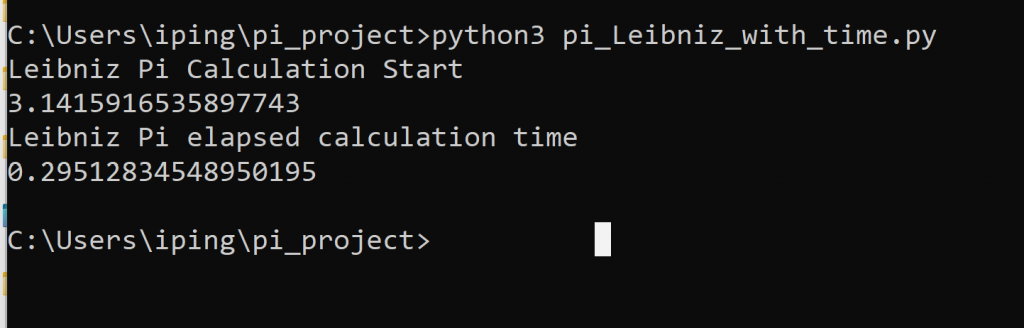
I was able to get a rudimentary calculation in Windows using both of the formulas and include a function to time the process consistently. Now I need to compare in Linux and blow out the calculation to allow a material number of places for this to be an effective measure.
I have found a few more options thanks to StackOverflow and I’m testing them now on my 12th Gen Intel machine.
- 100,000 digits of Pi using the “much faster” method proposed by Alex Harvey: 177.92 seconds for the first pass, 177.83 seconds for the second pass. I like the consistency
- Guest007 proposed an implementation using the Decimal library. I attempted a 10,000 digit calculation and that took 24.6 seconds, 100,000 places didn’t complete after more than 10 minutes. Interestingly, a peek at the system processing said it was only running 8.1% of CPU time.
Tomorrow I’ll start a new chart comparing these two methods across multiple machines.